力の神秘（しんぴ）


　美しいチューリップやカーネーションやヒヤシンス、ゼラニウム、シクラメンなどの花をあつめ、外をアスパラガスの葉で包んだ花束を持ったヒトミと東助が、雑草ののびた野原のまん中さしてはいっていく。
　いわずともみなさんはごぞんじ、今日は二人がポーデル博士を訪問する日だ。博士は月に一度、二人をふしぎな国に案内してくださる。先月は海底都市へ連れていってもらった。先々月は大宇宙のはてまで案内してもらった。さて今月はどんなふしぎな世界にひっぱっていってくださることだろうかと、二人は足をいそがせる。
　樽ロケットに腰をかけていたポーデル博士が立上って、二人の方へ手をふった。
「先生、こんにちは」
「先生。今日は花束をさしあげようと思って持ってまいりました」
「ほう、ほう。なかなかきれいな花です。たくさんの花です。ありがとう、ありがとう」
　ポーデル博士は、ひげをゆすって、うれしくてたまらないという風に、にこにこ顔。
「それでは、これを樽ロケットの中の花活（はないけ）にいけましょう。さあヒトミさんも東助君も、いっしょにおはいりなさい」
　みんなは、樽ロケットの中へはいった。
「先生。今日はどんなにふしぎな国へ連れていって下さるのですか」
「今日はですね、ふしぎな力の国へご案内いたします」
「ふしぎな力の国って、どんなところですの」
「みなさんは、ここにＡとＢと、二つの物があるとき、この二つの間に、引力（いんりょく）という力がはたらいて、たがいにひっぱりっこをしていることを知っていますか」
「引力なら、知っています」
「よろしい。その引力の法則を知っていますか。ニュートンが発見したその法則です。どうですか、東助君」
「引力の法則は、だれでも知っていなくてはならない法則だから、ぼくもよくおぼえていますよ。――二ツノ物体ノ間ノ引力ハ、ソノ二ツノ物体ノ質量ノ積（せき）ニ比例シ、二ツノ物体ノ距離ノ自乗（じじょう）ニ反比例（はんぴれい）スル。――これでいいのでしょう」
「それでよろしいです。つまり、ここに物体Ａと物体Ｂの二つだけがあったとします。物体の間には引力がはたらくのです。その引力の大きさは、今も東助君がいったとおり、ＡとＢの質量――これは重さのことだと考えていいのですが、大きければ大きいほど、引力は大きい。また、ＡとＢとがどのくらいはなれているか、その距離が近ければ近いほど、引力はずっと大きい。距離が遠くなると、引力はずっと小さくなる。この距離と力の関係のことを、今日はとりあげて、おもしろい光景をお見せしますが、これはなかなか人類にとって、ありがたい法則なのであります」
「先生。今日はお話がむずかしくて、よく分りませんわ。もう一度いって下さい」
「ほう、ほう。そんなにむずかしいことありません。引力の法則などというから、むずかしく聞えますが、そんなに頭をかたくしないで、私のいうことだけ、考えてみて下さい」
「はい。そうします」
「いいですか、ヒトミさん。引力はね、物体Ａと物体Ｂの距離の自乗に反比例するのです。ははは、それ、むずかしい顔になりました。それ、いけません――。ＡとＢの距離が一メートルの場合と二メートルの場合と、引力は、どんなにちがうか。それを今申した法則をあてはめて、考えてみましょう。ヒトミさん、あなた計算してごらんなさい。わけなく、できます」
　ヒトミは、小首をかしげたが、おずおずと口をひらいた。
「二つの物体の距離に――いや、距離の自乗に反比例するのですから、距離が一メートルの場合は一の自乗はやはり一です。この一に反比例するんだから、分数にして、一分の一。一分の一はやはり一です」
「それから距離二メートルの場合は、どうなりますか」
「二メートルの場合は、二の自乗というと、二に二をかけることだから、二二が四で、四です。反比例だから、この四の逆数（ぎゃくすう）は、四分の一。小数にして〇・二五です。これでいいでしょうか」
「計算はいいですが、その意味はどうなりますか」
「さあ……」
「ＡＢの距錐が一メートルのときは、引力は一。二メートルはなれていると〇・二五。ですから、距離が二倍になると、引力は四分の一になるのです。もし距離が三メートルになって、三倍になると、引力の方は九分の一、つまり、〇・一一に弱まります。分りますか」
「ええ。分ったような、分らないような……」
「それでは、図にかいてみましょう。そうすると、よく分るでしょう」
　博士は席を立って、奥へいった。


　　　隕石落下（いんせきらっか）


　まもなく博士は、巻いた紙を持ってきた。
「これをごらんなさい。図面が三つありますよ」
　博士が紙をひろげると、（イ）と（ロ）と（ハ）の三つの図面が並べてあった。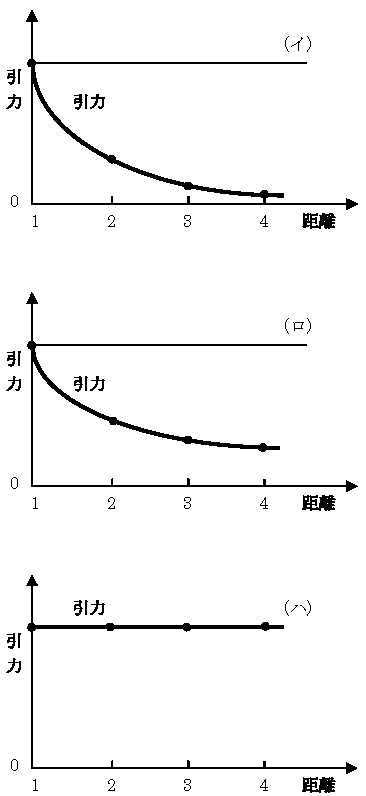
「この（イ）の図が、今考えた距離の自乗に反比例する場合です。太い曲線が、がけのように下りていますね。その曲線の高さが引力をあらわしています。距離が一メートルのところでは引力が一。二メートルでは〇・二五。三メートルでは〇・一一と、急に引力が小さくなっていきます。そのことがこの図で分るでしょう」
「ええ、分りますわ」
「（イ）の場合は、距離の自乗に反比例しましたが、（ロ）の場合は、距離に反比例するとしたら、どうなるだろうか、それを図にしてみたのです」
「自乗に反比例ではなく、ただ『反比例』する場合のことですか」
「そうです。ですから、（ロ）の場合は、ＡＢの距離が一メートルなら、その逆数は一。距離が二メートルなら、その逆数で二分の一。つまり〇・五ですね。距離が三メートルなら、その逆数で三分の一。つまり〇・三三。（ロ）の場合の曲線と、前の（イ）の場合の曲線とをくらべてみますと、（ロ）の方がずっと、いつまでも力が減りませんね」
「ええ」
「そうでしょう。距離一メートルのところでは、どっちも同じですが、距離三メートルになると（イ）の場合は〇・一一に減るのに、（ロ）の場合は〇・三三にしか減らない」
「ポーデル先生。そんな計算ばかりしていて、それがどうなるのですか。早くふしぎの国へ連れていって下さい」
　東助が、すこしたいくつの顔であった。
「この計算がね、ふしぎの国の案内書でありますよ。われわれは、（イ）の法則の世界に住んでいるから幸福なので、もし（ロ）の法則の世界に住んでいるとしたら、とてもそうぞうしくて、胸がどきどき、頭がぴんぴん、神経衰弱になるでしょう。それからまた（ハ）の法則の世界に住むならば、神経衰弱どころではなくて、けがばかりしていなければならないでありましょう。われわれは（イ）の法則の世界に住んでいるから、たいへんしずかで、安全であります」
「その（ハ）の法則の世界というと、どんな法則なんですの」
「おお、まだ説明しませんでしたね。（ハ）の場合は、ＡＢ間の引力が距離に無関係な場合であります。つまり距離が近くても遠くても、引力は同じにはたらくのです。すると、距離に無関係で、ただＡＢとの質量の大きさだけで、引力がきまります。そうなると、うるさいですよ」
「どんなにうるさいですか。そのような世界があったら、早く連れていって見せてください」
「それでは、その世界へいってみましょう。（ハ）の場合ですよ。引力が、距離に無関係である世界です。重ければ重いほど、引力が大きいという世界です。ほら。私が、ワン、ツー、スリーというと、その世界へ、みなさんがたは、はいってしまいますよ」
　そういったポーデル博士は、手を大きくふって、「ワン、ツー、スリー」と号令をかけた。
　すると今まで見えていた樽ロケットの中の一室が、とたんにぱっと消えた。そしてヒトミと東助とは、にぎやかな町のまん中にいた。
　とつぜん、どすんどすんと、大きな音がした。音のした方を見ると、大きなビルディングの屋上に近いところから、土けむりがあがり、建物の一部がこわれて、ばらばらと下に落ちてくる。
　あっ、通行人がたおれた。けがをしたんだ。バスが、ぺちゃんこになった。建物のかけらが、満員のバスの上に落ちたからだ。
「ややッ、たいへんだ。どうしたんだね」
「隕石（いんせき）のでかいのが落ちてきたんだ。めずらしいできごとだ」
　といっているとき、またもや大怪音（だいかいおん）だ。さっきのよりも、もっと大きい。
「おお、えらいことだ。五十五階の摩天（まてん）ビルが半分に折れて、あれあれ、あのようにこっちへ倒れてくるぞ。早くにげろ」
「どうしたんだ。あんな丈夫なビルが、二つに折れるなんて」
「とても大きい隕石（いんせき）が、ビルにぶつかったんだ。あたご山ぐらいの大きい隕石だったぜ。あんな大きなものにぶつかっては、どんなビルだってたまりゃしない。ああ、いけねえ、早くにげろ」
　ものすごい音響、つづいて、天地もくらくなるほどの土煙。東助はおどろいて、ヒトミの手をとってにげだした。
「どうしたんでしょうね、東助さん」
「あのことだよ。（ハ）の場合だよ。つまり引力は距離に無関係になったんだ。だから、どんな遠いところにあるものも近いところにあるものも、同じに引力がはたらくんだ。引力の大きさは、ただ、そのものの質量だけに関係するんだ。ということはね、軽い物は重いものにひきつけられるということなのさ」
「で、どうしたの、それが」
「だから、地球は大きいし、空をとんでいる隕石は小さいだろう、地球が隕石をみんなひきよせているんだよ」
「だって、今まででも流星（りゅうせい）というものがあって、隕石も落ちたでしょう。しかしこんなにたくさん落ちなかったわねえ」
「今までは、空の遠くをとんでいる隕石は、少しは地球の方へは引かれるけれど、遠くにあるものだから、結局、距離の自乗に反比例するという引力の法則によって、地球にはそれほど引きつけられず、他の方向へはずれていったんだよ。ところがね、（ハ）の場合だから、引力は距離関係がなくなり、重いものはどんどん軽いものを引張（ひっぱ）りつけることになったので、隕石はみんなこの地球へ引きよせられるのさ。まだまだ、たくさんの大きな隕石が降ってくるよ。地下室へはいらないと、あぶない」
「あれは何でしょう。空に大きな丸いものが見えますわ。あ、だんだん大きくなる。お月さまのようだけれど、お月さまにしては大きすぎるし……」
「たいへんだ。お月さまも、地球へ引張られて、こっちへ落ちてくるんだよ。これはたいへん、地球と月が、衝突する。地球がこわれてしまう。ぼくたちは死んじまうよ」
「ああ、困った。ポーデル先生」

 << 上一页  [11] [12] [13] [14]  下一页 尾页