［＃ここで表組終わり］
などが見つかる。「象」の訓キサと似たのにはマライの gajah（サンスクリットからとある）があるが、ゾウといったようなのはずいぶん捜したがなかなか見当たりにくくて、それが、どうであろう、突然こんな意外な所に現われたのである。「魚」も同様であった。「鳥」はむしろアイヌの chiri に近いから妙である。土佐（とさ）で咽喉（のど）を切って自殺する事を「フロヲハネル」と言うが、この「フロ」が偶然出て来たのはずいぶん人を笑わせる。もっとも万一ことによると、これはアラビアの halq その他同系の語を通じて結局は西欧の gorge, throat, Hals などにもつながり、また一方たとえばベンガリの gal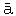 などを通してかなり東洋にも広がっているのかもしれないと想像される。もっと空想をたくましくすれば邦語のゴロなどというのも少しは怪しくなるくらいである。（鳥のアラビア語 tair. ［＃「t」は下点付き、182-6］咽喉（のど）のシナ語 hou lung）。
　こういう種類のではたとえばたっつけ袴（ばかま）のカルサンというのがインドへんから来ているかと思うと、イタリアにも類似の名が出て来たりするのである。（タミール語 Kalisan. イタリア語 Calzoni）。
　しかしこれらの例をあげたのは、決してこれらの語が邦語と因果的に関係しているという事を証明するためではなく、むしろただいかなる任意の二つの国語を取って比較しても、この種の類似がありうるものであるという事の例として取ったに過ぎない。それでたとえば、他方で「魚」や「鳥」の訓がシナ語や台湾語で説明されるとか、されないとかいう事は、ここでは問題にならないのである。
　ともかくも自分の皮相的な経験によると、いかなる国語の語彙（ごい）の比較でもあまりにおもしろい「発見」があり過ぎるような気がするので、これは少し考え方を変えなければならないという事に気がついた。そう思わせるもう一つの根拠に、ＡＢ両国語で互いに同じような音をもっていながら意味のほうでは明白になんの関係もないという例が、またかなりに多い。最も滑稽（こっけい）な例をあげるとフィンランド語では鶴（つる）が haikara であり、狼（おおかみ）が susi である。いかにこじつけたくても、フィンランドの鳥獣と東京の高襟（ハイカラ）や、江戸前の鮨（すし）とを連結すべき論理の糸は見つからない。しかしそうなると同じフィン語の狐（きつね）が kettu であり、小船が vene であり、樺（かば）が koivu であっても、これらの類似の前二者の類似との間の本質的の差を説明すべきよりどころがわからなくなるのである。
　浜の真砂（まさご）の中から桜貝を拾う子供のような好奇心の追究を一時中止して、やや冷静に立ち帰って考えてみると、これはむしろなんでもない事のようである、統計数学上の込み入った理論を持ち出すほどでなくとも、簡単なプロバビリティの考えから、少なくも原理の上からは、説明のつく事である、というふうに考えられて来た。
　まず試みに、子音にのみ注目するとする。そうしてＡの国語における子音の総数をｎとする。次に問題をできるだけ簡単にするためにＢ国語の子音をもこれと同数だとする。さらにいちばん簡単な場合を考えて、各子音がそれぞれ各国語に出現する頻度（ひんど）あるいは確率が一様で、皆νに等しいとすると、ν = 1/n ［＃「1/n」は分数］で均一になる。（これは少し乱暴に見えるかもしれないが、統計的方法では多くの場合近似の一法として許される事である。場合により頻度の著しく小さいものは省略する事もやってみてよい。）次に語彙（ごい）中で子音一つより成るもの、二つ、三つ、四つよりなるものというふうに分類する。そしてそれらのおのおのがＡＢ両国語に現われる確率をそれぞれ a1 a2 a3 …… b1 b2 b3 ……［＃アラビア数字はすべて下付き小文字］で示すとする。さすればＡ語のうちｉ個の子音より成るものの中のある一つを取って、それと同義の語がＢ語でも同じｉ個の子音の同順の排列からなるという事の確率は biνi［＃２文字目の「i」は下付き小文字、４文字目の「i」は上付き小文字］ であると考える事ができる。（無論Ａでｉが２のものを取る場合、Ｂでｉが２でないものはこの統計には入れない事にするのである）。ただしこれはＡ語一つに対するＢ語に同じｉ級のシノニムが他にないと仮定する場合で、もしシノニムがそれぞれ si［＃「i」は下付き小文字］ 個ずつあるとすればこの確率は si［＃「i」は下付き小文字］ 倍に増加する。もしこの上にメタセシスを許し、またＡ語の一子音に対すべきＢ語子音の転訛（てんか）範囲（はんい）を拡張すればこれはさらに増加する。それがいかに増加するかは計算しようと思えばされるはずのものである。しかしここでは最も簡単な場合として、同数シノニムというまでにとどめると結局ＡＢ両国（りょうこく）語彙（ごい）一般の比較によって得らるべき純偶然的一致の確率は、

で与えられるはずである。この中に出現するｓ、ａ、ｂ、νの各数はともかくも統計的になんとかして求められうる性質のものである。
　以上はできるだけ事がらを簡単に考えた考え方である。これ以上にだんだん試験的、近似的仮定を修正して、少しずつ実際の場合に近づけて行く事も、原理上からの困難はなく、ただ次第に計算が込み入るだけである。しかし、今のところ、あまりに込み入った計算では実用にならないから、できるならば簡単な形で進みたい。
　それで第一の試みとしては、まず前記のいちばん簡単な場合になるべく適合するように、材料のほうを選定し排列する事である。それはたとえば両国語の適当な語彙から比較に不適当な分子、たとえば本質的でないと思わるる接頭語、接尾語などを整理し（もちろんこれにはある仮定を要するが、それが tentative method として許容される事は、いわゆる精密科学においても同様である。そしてこの仮定には従来言語学者の苦心研究の結果が全部有効に利用されるはずである。）そうしてそれについて上記のａｂを出し、ｓは「近似的平均値」を推定して導入する。ここでいちばん困難なはＡＢのｎを同一に整理する事であるが、これにもいろいろの方法がある。たとえばＡ日本語とＢ英語の場合ならば、まず日本語のほうを、かりに「日本式ローマ字」で書く、しかして英語子音の「文字」の中で日本式にないものはかりに後者のどれかで「置換」する。たとえばｃやｑを皆ｋに直す類である。複子音も同様である。ｘなどは省いても、何かで置換しても統計の結果の値にはたいした影響は与えない事は明らかである。アラビアなどとなると、だいぶこの置換が困難な問題となるが、しかしたとえば喉音（こうおん）のあるものは半数だけｋかｇ、残り半数をｈで代用するというような試験的便法を取って第一歩を進める事もできる。（ここに統計的方法の長所があるとも言われる。）またたとえばマライ語の場合ならば ber, mer, per などのプレフィックスのｒを省いてみるとか、中間のngを省いてみるとかする事も試みてよいわけである。
　かくのごとき試験的（テンタティヴ）の整理によって、ともかくも両国語の子音がそれぞれかりに十四になったとする。次にかりに a1 a2 a3 a4 b1 b2 b3 b4［＃アラビア数字はすべて下付き小文字］ がいずれも１／４［＃「１／４」は分数］で a5 b5［＃「5」はすべて下付き小文字］ 以上は零とし、s1 s2 s3 s4［＃アラビア数字はすべて下付き小文字］ が平均皆４だと仮定すると
すなわち、指定のごとき比較によって、全然偶然から来る暗合の率が約二プロセントはできる事になる。
　しかし、上の仮定で明らかに最も不都合なのは、子音ただ一つをもつ語の割合をはなはだしく大きく見すぎた事である。これはシナ語の場合のほかには明らかに適用されない。
　それで、かりに、単子音語の確率を著しく小さいとして度外視し、なお次のごとく仮定する。
すなわちわずかに〇、四プロセント弱ぐらいに減じてしまうのである。
　なお、もしも、シノニムの数が、上記４の二倍であるとすれば、以上の百分値はやはり二倍になるだけであるから、このほうから結果の桁数（オーダー）に著しい影響は起こらない。
　次に特別な場合として、邦語をかな一つ一つに切り離し、その一つ一つと音韻の似た原語と同義のシナ文字を求め、それを接合して説明をするという、普通よくあるやり方をするとどうなるか。この場合は、a1 b1［＃「1」はすべて下付き小文字］ いずれも１で他は零となるから
しかるにシナでは異音類義の字が多いからこの s1［＃「1」は下付き小文字］ が大きくなりうる。かりに s1［＃「1」は下付き小文字］ を５とすると、三五、七プロセントという多数の暗合を見る事になる。これはこの種の方法による比較の価値を判断する際に参考になると思う。なおこの場合に同じ漢字の発音に対して、各地方的発音の異なるものを材料として、その中から都合のいいものを採るとなると s1［＃「1」は下付き小文字］ がさらにいっそうはなはだしく大きくなって、結局どうでもなるという事になり、かくのごとき比較の言語学上の価値はきわめて希薄になって来る事は明らかである。
　次に比較の標準を少し下げて、メタセシスを許容すると、Ｐの展開式のｉ項に※［＃「ｉ」の左側と下側を線で囲った記号、187-9］が乗ぜられる事になるが（ただし子音が皆異なるとして）、これでは少なくもｎがあまり小さくない限り、明らかに最後の結果の桁数（オーダー）に変化は起こらない。
　次に、子音転訛（てんか）を拡張して行くと、上記のｎが減少し、νが増加するから、これはＰに重大な影響を及ぼす事となる。かりに濁音を清音と同じにしたり、ｋとｈ、ｍとｂ、ｓとｔなどを同一視したりいろいろして行くと、独立したものの数ｎは僅々（きんきん）五つか六つになってしまう。従って最後のＰは著しく増大する。たとえば、ｎを５とすると
であるから a1 = b1 = 0; a2 = b2 = a3 = b3 = 4/10; a4 = b4 = 2/10［＃アルファベットに続くアラビア数字はすべて下付き小文字、「4/10」「2/10」は分数］ の場合でも、P = s×0.007744 となり、ｓが４ならば、約三、一％を得るわけである。すなわち、三分ぐらいの符合では偶然だか、偶然でないかわからない事になる。
　以上はもちろんかなりいろいろな無理な仮定のもとに行なった計算である。これを逐次修正して言語学者の要求に応ずるように近づけて行くことは必ずしも困難ではないが、ここではしばらくこれ以上に立ち入らない事にする。
　要するにこれは、表題にも掲げたとおり、比較言語学上における統計学的研究の可能性を暗示するための一つの試みに過ぎないのである。
　学者の中には、二つの国語の間の少数な語彙（ごい）の近似から、大胆に二つのものの因果関係を帰納せんとする人もあるようであり、また一方においてあまりに細心で潔癖なために、暗合の悪戯に欺かれる事を恐れてこの種の比較に面迫することを回避する人もあるかもしれない。自分にはこの二つの態度がいつまでも互いに別々に離れて相対しているという事が斯学（しがく）の進歩に有利であろうとは思われない。むしろ進んで、暗合的なものと因果的なものとを含めた全体のものを取って、何かの合理的な篩（ふるい）にかけて偶然的なものと必然的なものとを篩（ふる）い分ける事に努力したほうが有利ではあるまいか。そうして統計的に期待さるべき暗合の確率と、実際の統計的符合率とを対照して、因果関係の「濃度」を示すべき数値を定め、その値の比較的大なるものについて、さらに最初の仮定の再吟味を遂行し、その結果に基づいて修正された新たな仮定を設け、逐次かくのごとくしていわゆる漸近的近似法によって進行すれば、少なくも現在よりは、いくらか科学的に研究を進められはしないかと考えるのである。
　たとえば子音転訛（てんか）の方則のごときでも、独断的の考えを捨てて、可能なるものの中から甲乙丙……等の作業仮定を設けて、これらにそれぞれ相当するＰを算出し、また一方この仮定による実際の比較統計の符合の率を算出し、この両者を比較して、その結果から甲乙丙いずれが最も穏当であるかを決定すべきである。
　統計的方法の長所は、初めから偶然を認容してかかる点にある。いろいろな「間違い」や「杜撰（ずざん）」でさえも、最後の結果の桁数（オーダー）には影響しないというところにある。そして、関係要素の数が多くて、それら相互の交渉が複雑であればあるほど、かえってこの方法の妥当性がよくなるという点である。
　それで、この方法を真に有効ならしむるには、むしろあらゆる独断、偏見、臆説（おくせつ）をも初めから排する事なく、なるべくちがったものをことごとくひとまず取り入れて、すべての可能性を一つ一つ吟味しなければならない。軽々しい否定は早急な肯定よりもはるかに有害であるからである。これは実験的科学を研究する者に周知の事である。また往々にして忘却される事である。もっともこういうたんねんの吟味をするにはかなりの手数と時間を要する。それかと言って、いつまでもなんらかこの種の方法をとらなければ、独断と独断との間の討論の終結する見込みは立たないように思われるのである。いかにめんどうでも遂行すればするだけ、あともどりはしないであろうと信ずる。しかもそのほう専門の研究者の専門の仕事として見る時は、他の科学者、たとえば天文学者、物理学者、化学者などの仕事に比してそれほどにめんどうな仕事とは決して思われないのである。
　もちろん、これも他の科学の場合と全く同様に、初めからそううまくは行かないであろう。そうして、すべての可能なるものへの試みの「不可能」を「証明」し、抹殺（まっさつ）する事にのみ興味をもつ「批評家」の批評を受けなければなるまい。しかしあらゆる「精密科学」はその根底において、ちょうどかくのごとき方法を取って進んで来たものである。すべてがそのはじめは不精密なる経験の試験的整理を幾重となく折り返し繰り返し重ねて、漸進的に進んで来たものである。その昔、独断と畏怖（いふ）とが対峙（たいじ）していた間は今日の「科学」は存在しなかった。「自然」を実験室内に捕えきたってあらゆる稚拙な「試み」を「実験」の試練にかけて篩（ふる）い分けるという事、その判断の標準に「数値」を用いるという事によって、はじめて今日の科学が曙光（しょこう）を現わしたと思われる。もし古来の科学者が、「試み」なしの臆断（おくだん）を続けたり、「試み」の結果を判断する合理的の標準なしに任意の結論を試みたり、あるいは「試み」に伴なう怪我（けが）のチャンスを恐れて、だれも手を下す事をあえてしなかったら、現在のわれわれの自然界に関する知識と利用収穫は依然として復興期以前の状態で足踏みをしていたであろう。そしてまた現在の進歩した時代から見た時に幼稚に不完全に見えないものがいかなる初期の科学の部門に見いだされうるであろうか。
　余談はしばらくおいて、ＡＢ、ＡＣ、ＡＤ……の関係、なお念のために比較の主客を置換してＢＡ、ＣＡ、ＤＡ……の関係の濃度に対するだいたいの比較的の数値を定める事ができたとすれば、少なくもここにＡＢという一つの「鎖の輪」が、従来よりはやや科学的な根拠の上に仮設される。さすれば次には、前にＡについて行なったと同様の方法を、今度はＢについて行なうべきである。そうしてともかくも、ＢＣという、「次の輪」の見当をつける。順次かくのごとくして、できるならばまた、世界の各方面から出発して、同じようにして、それぞれの鎖を――もちろんそういう鎖が存在するとの作業仮設のもとに――たぐって行く。もし多くの人の信ずるであろうごとく、この数々の鎖が世界のどこかに自然と集合すれば簡単である。さすればその焦点に集中した要素をやや確かに把握（はあく）し得らるるから、今度は逆の順序によってこの焦点から発散し拡散した要素の各時代における空間的分布を験する事ができる、その時に至ってはじめて、この編の初めに出した拡散に関する数式がやや具体的の意義を持って現われて来るであろう。もっともそれはできるとしてもはなはだ遠い未来において始めて実現されうる事であろう。
　しかし上に考えた鎖はおそらく一点には集中しないであろう、それがどう食い違うか、そこに最も興味ある将来の問題の神秘の殿堂の扉（とびら）が遠望される。この殿堂への一つの細道、その扉を開くべき一つの鍵（かぎ）の、おぼろげな、しかも拙な言葉で表現された暗示としてのみ、この一編の正当な存在の意義を認容される事ができれば著者としてむしろ望外の幸いである。
　自分はできるだけ根拠なき臆断（おくだん）と推理を無視する空想を避けたつもりである。しかし行文の間に少しでも臆断のにおいがあればそれは不文の結果である。推理の誤謬（ごびゅう）や不備があればそれは不敏のいたすところである。このはなはだ僭越（せんえつ）と考えらるべき門外漢の一私案が、もし専門学者にとってなんらかの参考ともならば、著者としての喜びはこれに過ぎるものはない。
　思うにこの私案の第一歩の試みを最も有効に遂行するためには、おそらく言語学者と科学者との協力が必要ではないかと思われる。もしこの両者が共同し、その上に機械的の計算や統計を担当する助手の数人の力をかりることができれば、仕事はかなりおもしろく進行しそうに思われる。しかしこのほうがむしろおそらく夢のような空想であるかもしれない。

　（付記）　以上の考察においては、最もこの種の取り扱いに便宜だというだけの理由から、単に「語彙（ごい）」「単語」のみを問題として、語辞構成法や文法上の問題には少しも触れなかった。しかし自分は決して後者の比較の重要な事を無視しているのではない事を断わっておきたい。もっとも文法のごときものでも、これを数理的の問題として取り扱う事が必ずしも不可能とは思われない。事がらが、見方によってはある有限数の型式的要素の空間的排列の方式に関するものであると見る事ができるからである。輓近（ばんきん）の数学の種々な方面の異常な進歩はむしろいろいろな新しいこの方面の応用を暗示するようである。また「除外例」というもののある事から起こる困難は、統計的方法の利器によって、少なくもある度まで救われうる見込みがある。これについては、さらに、機会があったら、いくぶん具体的に考えを進めてみたいという希望をもっている。
　最後に誤解のないために断わっておく必要のあるのは、従来とても統計的のやり方はあるにはあるが、単に数をかぞえて多いとか少ないとかいうだけではなんらのほんとうの統計としての意味がないという事である。全体に対する実際の符合率が偶然による符合率に対する比のみが意味をもつ、ここではそれを問題にしたという事である。

上一页  [1] [2]  尾页