私はこのような考えを正す目的で、時々最寄（もよ）りの停留所に立って、懐中時計を手にしては、そこを通過する電車のトランシットを測ってみた。その一例として去る六月十九日の晩、神保町（じんぼうちょう）の停留所近くで八時ごろから数十分間巣鴨（すがも）三田（みた）間を往復する電車について行なった観測の結果を次に掲げてみよう。表中の時刻は、同停留所から南へ一町ぐらいの一定点を通過する時を読んだものである。時間の下に付した符号は乗客の多少を示すもので、これはほんの見当だけのものである。○はいわゆる普通の満員、△は座席はほぼ満員だがつり皮は大部分すいている程度、×は空席の多いいわゆるガラアキのものである。◎は極端な満員、××は二三人ぐらいしかいないものを示す。

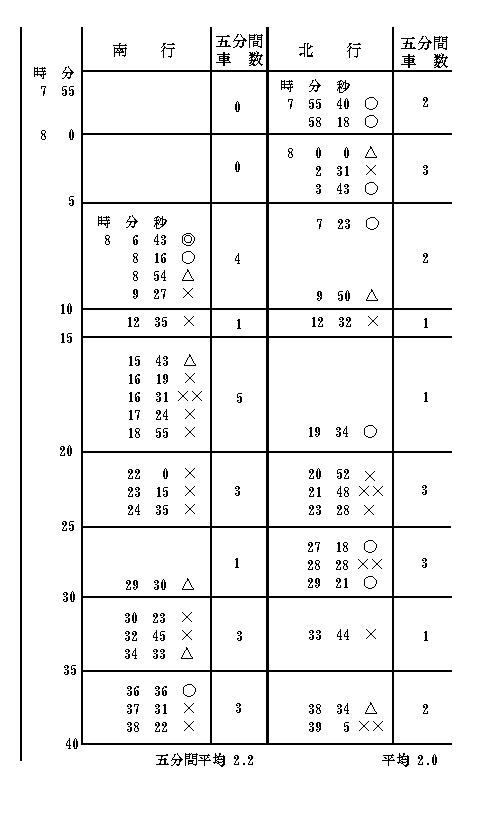
　この表で見ると、たとえば五分ごとに通る車数はかなりの変化があるにかかわらず、その平均数は北行南行ともにほぼ同様で、約二分半に一台の割合である。しかし実際の個々の時間間隔は、南行の最初における十一分三秒プラスという極端から、わずか十二秒という短い極端まで変化している。しかして多少の除外例はあるにしても、だいたいにおいて長い間隔の後には比較的混雑した車が来る事、短い間隔の後にはすいた車が来る事がわかるだろう。
　今これら各種の間隔の頻度（フリクエンシー）について統計してみると次のとおりである。

　これでわかるように、間隔の回数から言うと、長い間隔の数はいったいに少なくて、短いものが多い。全体三十八間隔の中で、四分以上のものは四回、すなわち全体の約一割ぐらいのものである。しかしここで誤解してならない事は、乗客がこれらの長短間隔のいずれに遭遇する機会（チャンス）が多いかという問題となると、これは別物になるのである。この点を明らかにするには、各間隔の回数に、その間隔の時間を乗じた積の和を比較してみなければならない。今試みに間隔を一分ごとに区別分類して、各区分内の間隔回数にその区分の平均時間数を乗じたものの和を求めてみると、かりに五分以上の間隔を度外視して計算してみても、二分以下のものに対して二分以上五分までのもののこの積分の比は二三、五と四六、五すなわち約一と二の比になる。もしこれに時々起こる五分以上の間隔を加えて計算すると、この懸隔はさらに著しくなる。
　これは何を意味するか。
　個々の乗客が全く偶然的に一つの停留所に到着したときに、ある特別な間隔に遭遇するという確率（プロバビリティ）は、あらゆる種類の間隔時間とその回数との相乗積の総和に対するその特別な間隔の回数と時間との積の比で与えられる。そこでたとえば前の例について言えば二分以下の間隔に飛び込む機会は三度に一度で、二分以上五分までの長い間隔にぶつかるほうは三度に二度の割合になる。実際は五分以上のものが勘定に加わるからおそらくこの割合は四度に三度ぐらいになる場合が多いだろうと思われる。（停留所で待つ時間の確率を論じるには、もう少し立ち入る必要があるが、これは略して述べない。）以上はただ一例に過ぎないが、私の観測したその他の場合にも、だいたいこれと同様な趨勢（すうせい）が認められるのである。
　それでともかくも、全く顧慮なしにいつでも来かかった最初の電車に飛び乗る人にとっては、すいたのにうまく行き会う機会が少なくて、込んだのに乗る機会が著しく多い。そういう経験の記憶が自然に人々の頭にしみ込む。おそらく込み合っていた多数の場合の記憶は、まれにすいていた少数の場合の記憶よりも強く印銘せられるとすると、以上の比例の懸隔は、心理的に変化を受け、必ずいくぶんか誇張されて頭に残るかもしれない。従って多くの人はついついすいた電車の存在を忘れて、すべてのものが満員であるような印象をもつ事になるかもしれない。
　この最後の点は不確かだとしても、次の結論は免れ難い、すなわち「来かかった最初の電車に乗る人は、すいた車に会う機会よりも込んだのに乗る機会のほうがかなりに多い。」
　このようにして、込んだ車にはますます多くの人が乗るとすれば、この電車はますます規定時間よりも遅れるために、さらにまた混雑を増す勘定である。
　これをせんじつめると最後に出て来る結論は妙なものになる。すなわち「第一に、東京市内電車の乗客の大多数は――たとえ無意識とはいえ――自ら求めて満員電車を選んで乗っている。第二には、そうすることによって、みずからそれらの満員電車の満員混雑の程度をますます増進するように努力している。」
　これは一見パラドクシカルに聞こえるかもしれないが、以上の理論の当然の帰結としてどうしてもやむを得ない事である。もしこれがおかしいと思われるなら、それは私の議論がおかしいのではなくて、そういう事実がおかしいのであろう。
　それでもしこのような片寄りがちの運転状況を避けて、もう少し均等な分配を得たいというならば、そのために採るべき方法は理論上からは簡単である。第一には電車の車掌なり監督なりが、定員の励行を強行する事も必要であるが、それよりも、乗客自身が、行き当たった最初の車にどうでも乗るという要求をいくぶんでも控えて、三十秒ないし二分ぐらいの貴重な時間を犠牲にしても、次のすいた電車に乗るような方針をとるのが捷径（しょうけい）である。これがために失われた三十秒ないし二分の埋め合わせはおそらく目的地に着く前にすでについてしまいそうに思われる。
　しかし満員電車をきらうか好くかは「趣味」の問題であろうから、多数の乗客がもし満員電車に先を争って乗る事に特別な興味と享楽を感じるならば、それはいたし方がない。その趣味の是非を論じるための標準は数理や科学からは求められない。
　昔は、人に道を譲り、人と利福を分かつという事が美徳の一つに数えられた。今ではそれはどうだかわかりかねる。しかしそういう美徳の問題などはしばらくおいて、単に功利的ないし利己的の立場から考えても、少なくも電車の場合では、満員車は人に譲って、一歩おくれてすいた車に乗るほうが、自分のためのみならず人のためにも便利であり「能率」のいい所行であるように思われる。少なくも混雑に対する特別な「趣味」を持たない人々にとってはそうである。

　これは余談ではあるが、よく考えてみると、いわゆる人生の行路においても存外この電車の問題とよく似た問題が多いように思われて来る。そういう場合に、やはりどうでも最初の満員電車に乗ろうという流儀の人と、少し待っていて次の車を待ち合わせようという人との二通りがあるように見える。
　このような場合には事がらがあまりに複雑で、簡単な数学などは応用する筋道さえわからない。従って電車の場合の類推がどこまで適用するか、それは全く想像もできない。従ってなおさらの事この二つの方針あるいは流儀の是非善悪を判断する事は非常に困難になる。
　これはおそらくだれにもむつかしい問題であろう。おそらくこれも議論にはならない「趣味」の問題かもしれない。私はただついでながら電車の問題とよく似た問題が他にもあるという事に注意を促したいと思うまでである。

上一页  [1] [2]  尾页